딥러닝(Deep Learning) 기본

딥러닝(Deep Learning)

딥러닝은 기계학습의 한 종류입니다. 심층학습이라고도 합니다. 딥러닝의 다른 이름은 인공심층신경망(Artificial Deep Neural Network)입니다. 인공신경망(Artificial Neural Network)의 일종이라고 볼 수 있습니다. 딥러닝을 이해하기 위해서는 인공신경망에 대해 알아볼 필요가 았습니다.

인공신경망(Artificial Neural Network)

인공뉴런(Artificial Neuron)

인공신경망은 인공뉴런(Artificial Neuron)이라는 특정한 형태의 수학적인 함수로 이루어져 있습니다. 인공뉴런은 논리와 계산을 바탕으로 하는 순전히 수학적인 개념입니다. 인공뉴런을 단순하게 함수로 생각하고 수식으로 표현하면 아래와 같습니다.

인공뉴런은 입력값 \(X(x_1, ..., x_m)\)에 대하여 출력값 \(o\)를 갖는 함수입니다.

\[ h = \sum_{i=1}^m x_iw_i, \quad o = \begin{cases} 1, & \text{if } \text{ }\text{ } h \ge \theta \\ 0, & \text{if } \text{ }\text{ } h \lt \theta \end{cases} \]

풀어서 설명하며 입력값의 모든 원소(element)들에 계수를 곱해서 합을 구한 값이 \(h\)입니다. 이 \(h\)의 값이 특정 임계값 \(\theta\)보다 크거나 같으면 출력이 1이되고 작으면 0이되는 함수입니다. 이 함수는 뇌의 신경세포인 뉴런에서 영감을 얻어서 만들어진 함수이기 때문에 인공뉴런이라는 이름이 붙게 되었습니다. 생물의 신경세포인 뉴런의 구조는 아래와 같습니다.

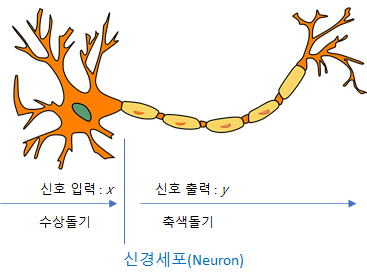
위 그림에서 신경세포는 수상돌기(Dendrite)라는 부분과 축색돌기(Axon)라는 부분으로 구성됩니다. 수상돌기는 여러개의 입력신호를 받는 역할을 하며 수상돌기에서 받은 모든 입력신호는 핵에서 처리된 후 하나의 출력이 되어 축색돌기를 통하여 다음 단계로 전달되는 것으로 알려져 있습니다. 입력신호가 어떤 형태로 오는지 그리고 어떻게 처리되는지 상세한 원리를 모르는 상태에서 수학적 상상력을 발휘하여 만든 것이 인공뉴런입니다.
위의 인공뉴런 수식을 도형 형태로 표시하면 다음과 같습니다.

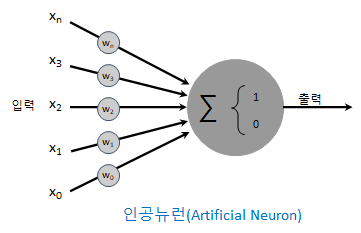
이 동형식이 의미하는 내용은 위의 수식과 동일합니다. 입력 부분의 화살표는 각각 입력값의 원소에 곱해지는 계수(\(w_n\))를 나타냅니다. 1943년에 워런 맥컬록(Warren McCulloch)와 월터 피츠(Walter Pitts)가 “A logical calculus of the ideas immanent in nervous activity”라는 논문에서 수학과 임계 논리(Threshold Logic)라 불리는 알고리즘을 바탕으로 신경망을 위한 계산학 모델을 발표하면서 인공뉴런이 등장하게 되었습니다. 인공신경망(Artificial Neural Network)은 이런 인공뉴런의 조합으로 만들어지는 함수들입니다. 하나의 인공뉴런도 단순한 형태의 인공신경망이라고 할 수 있습니다. 인공뉴런은 이 후 퍼셉트론(Perceptron)의 기반이 됨으로써 인공신경망 발전의 시초가 됩니다.

퍼셉트론(Perceptron)

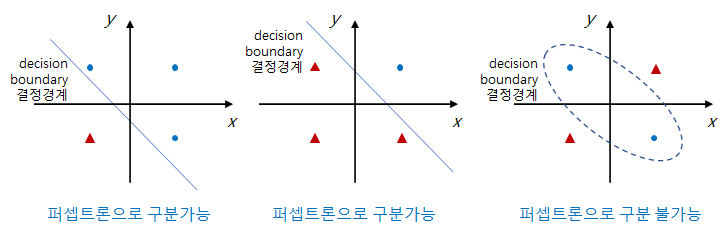
1957년 프랭크 로센블랫(Frank Rosenblatt)의 "The Perceptron : A Perceiving and Recognizing Automation(인식 자동화 장치)"라는 보고서에서 처음 등장한 개념입니다. 퍼셉트론은 간단한 인공뉴런을 기반으로 하여 주어진 데이터들을 두 종류로 분류할 수 있는 선형이진분류기(Linear Binary Classifier)입니다. 이 것을 그림으로 표현해 보면 아래와 같습니다.

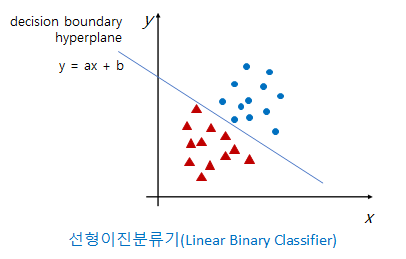
선형이진분류기란 위 그림에서 파란색 점들과 빨간색 세모들을 구분하는 직선을 말합니다. 이 직선의 위쪽에 있는 데이터는 파란색 점이고 아래쪽에 있는 데이터는 빨간색 세모라고 판단할 수 있습니다. 이 직선을 결정경계(Decision Boundary)라고도하며 일반화하여 초평면(Hyperplane)이라고 합니다. 퍼셉트론은 이 직선의 식을 표현합니다. 2차원 평면에서 직선의 식은 x, y의 계수와 상수항으로 결정할 수 있습니다. x, y를 \(x_1\), \(x_2\)로 바꾸어 표현하면 다음과 같이 쓸 수 있습니다.

\[ ax + by + c = 0 \\ w_1x_1 + w_2x_2 + w_0 = 0 \]

이러한 선형분류기를 찾고 크기 비교를 통하여 주어진 입력 데이터에 대하여 어떤 종류(Class)에 포함되는 지 결정하는 함수가 퍼셉트론입니다. 퍼셉트론을 앞에서 본 도형의 식으로 표현하면 다음과 같습니다.

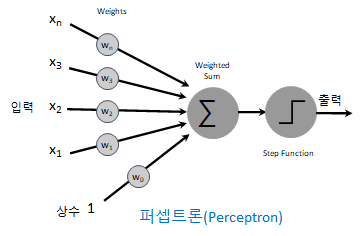
그림에서 보이는 것처럼 퍼셉트론은 인공뉴런의 일종입니다. 인공뉴런의 기능을 구체화하고 명확하게 하였습니다. 입력값의 모든 원소에 대하여 각각의 계수값을 곱하고 상수항(\(w_0\))과 함께 더하여 전체합(weighted sum)을 구합니다. 그리고 이 전체합을 입력으로하여 임계값과 비교하여 출력값을 만드는 부분을 활성함수(Activation Function)로 분리하여 명확하게 하였습니다. 딥러닝에서는 이계수값들을 가중치(Weight) 또는 파라미터(Parameter)라고 합니다. 퍼셉트론은 이렇게 입력값에 가중치를 곱하여 합을 구한 후 활성함수를 통하여 최종 구분값(1, 0 또는 1, -1 등)을 출력하는 함수라고 생각하면 됩니다.
초기의 인공뉴런과 퍼셉트론을 차별화하는 점은 로젠블렛이 퍼셉트론의 개념을 소개하며 발표한 퍼셉트론 알고리즘입니다. 퍼셉트론 알고리즘은 두 가지 종류에 속하는 데이터들을 구분하는 결정경계의 방정식을 주어진 데이터를 가지고 훈련을 통하여 알아낼 수 있는 알고리즘입니다. 퍼셉트론 알고리즘으로 인하여 인공신경망이 올바른 데이터가 있을 때 스스로 학습할 수 있다는 가능성이 증명됩니다. 다만 퍼셉트론의 한계는 결정경계가 직선으로 이루어지는 선형분리 문제만을 풀 수 있다는 큰 약점을 가지고 있었습니다.

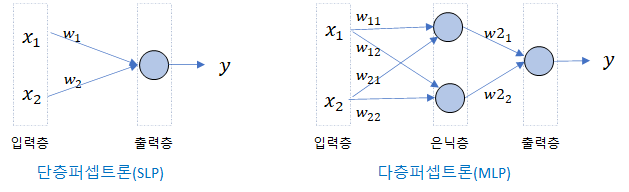
다층 퍼셉트론(MLP; Multi-layer Perceptron)

이런 퍼셉트론의 한계를 극복할 수 있는 방법으로 등장한 것이 다층퍼셉트론(MLP; Multi-Layer Perceptron)입니다. 위에서 본 퍼셉트론은 입력데이터에 한 번만 가중치들을 곱해서 합(가중합; Weighted Sum)을 구합니다. 이 때 데이터가 입력되는 부분을 입력층이라고 하고 활성함수를 통하여 출력값이 구해지는 부분을 출력층이라고 합니다. 위에서 본 단순 퍼셉트론을 단층퍼셉트론(Single Layer Perceptron)이라고 합니다. 이 입력층과 출력층 사이에 새로운 계산 계층을 추가할 수 있는데 이 계층을 입력층과 출력층 사이에 숨어 있다고해서 은닉층(Hidden Layer)이라고 합니다. 이런 은닉층이 하나 이상 추가된 것이 다층퍼셉트론(MLP)입니다. 다층퍼셉트론은 단층퍼셉트론이 가지고 있던 한계를 극복하여 비선형분리도 할 수 있는 해결책을 제시합니다. 아래 그림은 단층퍼셉트론과 다층퍼셉트론을 간략하게 도식화 한 그림입니다.

딥러닝(DL; Deep Neural Network)

위 그림과 같이 다층퍼셉트론은 입력층과 출력층 사이에 은닉층을 가지고 있습니다. 그림에서는 하나의 은닉층만 표시되었지만 은닉층은 필요에 따라 얼마든지 추가될 수 있습니다. 다층퍼셉트론과 같이 하나 이상의 은닉층을 가지고 있는 인공신경망을 심층신경망(Deep Neural Netowokr)이라고 합니다. 심층신경망의 다른 이름이 딥러닝입니다. 딥러닝이란 입력층과 출력층 사이에 하나 이상의 은닉층이 있어서 깊이가 깊은 구조의 신경망을 만들 수 있는 인공신경망을 의미합니다.
딥러닝은 이렇게 은닉층을 가지는 모든 종류의 인공신경망을 의미하며 딥러닝에는 앞에서 본 다층퍼셉트론 외에도 다양한 알고리즘을 이용한 어러가지 심층신경망 모델이 존재합니다. 가장 기본이 되는 딥러닝 모델들은 다음과 같습니다.

• 다층퍼셉트론 (MLP; Multi Layer Perceptron)
  • 가장 기본적인 타입의 딥러닝 모델입니다. 모든 유닛들이 연결되어 파라미터 수가 많습니다. 분류나 회귀분석, 자연어 처리 등 대부분의 경우에 사용될 수 있으며 계층을 많이 쌓거나 데이터가 많을 경우 계산량이 매우 많아 집니다.
    
• 합성곱신경망(CNN; Convolutional Neural Network)
  • 모든 유닛을 연결하는 파라미터를 사용하지 않고 커널(필터)라는 단위의 공용 파라미터를 사용하여 전체 파라미터의 수와 계산량을 줄인 모델로 이미지 처리에 적합하여 대부분의 이미지 처리에 사용됩니다.
    
• 순환신경망(RNN; Recurrent Neural Network)
  • 순서가 있는 시퀀스(sequence) 데이터에 적합한 타입으로 자연어처리에 많이 사용됩니다. 개량된 타입인 LSTM(Long-Short Term Memory)이 주로 사용됩니다.

이상 딥러닝이 무엇인지 간단하게 알아보았습니다. 딥러닝에 대해 더 깊이 있게 알아보고 기술적인 내용을 이해하기 위해서는 직접 실습을 해보는 것이 좋습니다. 딥러닝 시스템도 하나의 컴퓨터 소프트웨어이므로 코딩을 통해 프로그램을 직접 만들어 보는 것이 좋습니다. 사실 직접 만들어 보지 않고서 딥러닝에 대해 기술적으로 이해하는 것은 불가능할 것 같습니다.
다음에는 딥러닝을 기술적으로 더 깊이 있게 다루고 직접 코딩을 하는 방법에 대해 다루어 보겠습니다.